Long WordPress posts can be tough to read. How do you share detailed content without losing your readers’ interest?
The answer is post pagination, which means splitting a long post into several shorter pages. We’ve used this method to break up big guides and long tutorials in some of our blogging projects. Every time, we noticed readers engaged more with the content.
In this guide, we’ll show you how to split your WordPress posts into multiple pages. We’ll cover easy methods, with and without a plugin.
Why Split WordPress Posts Into Multiple Pages?
If you have WordPress blog posts or guides that are lengthy, then setting up WordPress pagination can improve the readability of your content.
It helps to break down a long post into different sections and split them into multiple pages. This way, visitors can easily digest your content and read any section they are interested in.
Another benefit of splitting WordPress posts is that it can boost your user engagement. When users navigate through paginated content, each page they view contributes to increased pageviews, which can positively impact your website’s overall metrics.
That being said, let’s take a look at how to split WordPress posts into multiple pages. We will cover how to break your WordPress posts into multiple pages without a plugin and using a WordPress plugin:
- Method 1. Split a WordPress Post Into Multiple Pages Without a Plugin
- Method 2. Split Multiple WordPress Posts Into Several Pages Using a Plugin
Method 1: Split a Single Post Into Multiple Pages Without a Plugin
The easiest way of setting up post pagination is by using the ‘Page Break’ block in your WordPress block editor. You don’t need a WordPress plugin to break up your articles into multiple pages.
First, you need to edit or add a new post on your WordPress website using the Gutenberg block editor.
After that, click the ‘+’ button where you want to split your content and add a Page Break block.
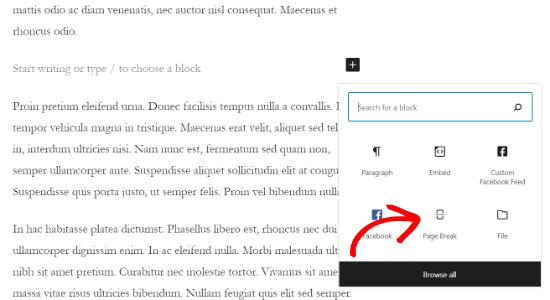
You should now see a page break line in your content to indicate where the pagination will appear.
It will look something like this.
If you are using the old classic editor, then you can use the <!––nextpage––> tag to split your content.
When writing a blog post, just go to the ‘Text’ editor view to enter the tag where you would like to split the long article.
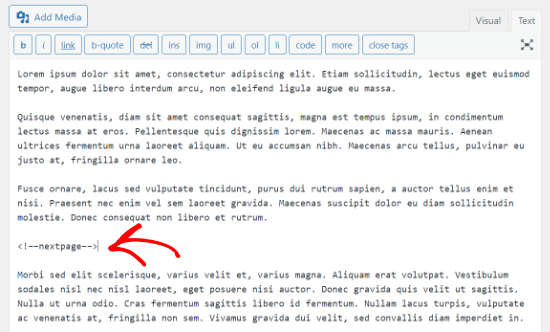
You can also use the Alt + Shift + P keys on your keyboard to insert page breaks. To do that, go to the ‘Visual’ view and press the keyboard shortcut keys where you want to add a page break.
After that, you can preview and publish the blog post. You will now see post pagination at the bottom of the post content.
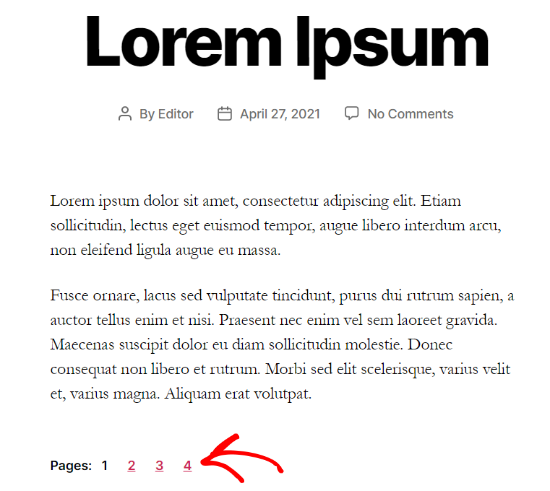
Method 2: Split Multiple WordPress Posts Into Several Pages Using a Plugin
Another way to break lengthy content into various pages is by using a pagination plugin. The benefit of this method is that it will automatically paginate posts when they meet certain criteria.
For this method, we will use the free Automatically Paginate Posts plugin, as it’s easy to use and works with any WordPress theme.
Note: You may notice that this plugin has not been tested with the latest WordPress versions. However, we’ve tried it ourselves, and it works the best out of all the plugins we’ve checked out.
You can read more about whether you should use untested WordPress plugins in our article. If you find a plugin that works better than the one we offered, then feel free to let us know in the comments below!
First, you need to install and activate the Automatically Paginate Posts plugin on your WordPress website. For more details, you can see our tutorial on how to install a WordPress plugin.
Once the plugin is active on your site, go to Settings » Reading and scroll down to the ‘Automatically Paginate Posts’ section.
You can select the post types to split into different pages. After that, choose whether to split posts by the total number of pages or approximate words per page.
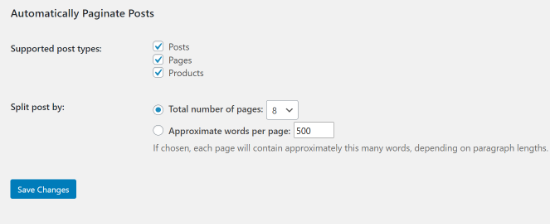
Next, click the ‘Save Changes’ button to store your settings.
The plugin will automatically split your content based on your settings. However, you can also add page breaks manually to your content while using the plugin.
Bonus Tip: Use AIOSEO to Optimize Your Post Pagination
Paginating your long post can definitely improve the user experience. That said, it’s important you configure the post properly so that it doesn’t negatively affect your site’s SEO (search engine optimization).
If a blog post is spread across multiple pages due to pagination, then Googlebot could end up indexing multiple copies of the same content. This can then lead to duplicate content issues.
Thankfully, you can avoid this by using the All in One SEO (AIOSEO) plugin. This WordPress SEO plugin makes it easy to make your site SEO-friendly, even if you have no technical expertise.
AIOSEO automatically inserts a page number into the SEO title of paginated content. This way, search engines can understand that the post has been spread across several pages and is not a duplicate of another post.
Furthermore, AIOSEO will remove these page numbers from the URLs of your post pages. Doing so will let search engines know the main blog post page that they should rank for the relevant keywords and users should see first.
It does this by automatically turning on the ‘No Pagination for Canonical URLs’ setting.
For more information about AIOSEO, please see our article on how to set up AIOSEO for WordPress.
More Tips for Managing Long Content in WordPress
Splitting posts into pages is just one way to handle long content. Here are some other useful techniques we’ve found helpful:
- Tooltips are great for adding extra details without cluttering your main content. They pop up when readers hover over certain words.
- Keep readers engaged by showing them related content right in the middle of your posts.
- If you have an extensive topic to cover, consider creating a post series instead of writing a long blog post about it. This helps readers follow along easily.
- Your post title is usually just a single heading, but you can break it into a new line if it’s too long to make it more readable.
We hope this article helped you learn how to split WordPress posts into multiple pages. You may also want to see our guide on how to add a load more button in WordPress posts and our expert picks of the best related posts plugin in WordPress.
If you liked this article, then please subscribe to our YouTube Channel for WordPress video tutorials. You can also find us on Twitter and Facebook.
maik
How to invert the pagination, I want create a page and spliting in multiples pages to show the recent posts? : This mode: 3, 2, 1. and no Pages 1, 2, 3.
semmy
Hi thank you very much for your tutorial. It’s work, oh ya I want to ask something about adsense, how we can add adsense below multiple pages, can you create a tutorial for that one? many thanks
Edwin
Thanks for the tip, I’ve recently tried this, and the pagination shows up correctly, but when clicking the links (2,3,4,etc.), i get a page not found error. Do you have any idea what would cause that?
Ricardo Cury
You might want to check you Permanent Links Structure.
Edmond
Hi,
Can you please do a tutorial on how to create the “view all” function too, as it’s really very useful. I’ve seen a similar thing here: http://list25.com/25-most-expensive-private-jets-ever-made/ (http://list25.com/25-most-expensive-private-jets-ever-made/?view=all)
Thanks!
Edmond
Hi,
Really love the feature of splitting pages. I also see that you have the “View All” option on list25.com. How can I add that same feature to my website? I’d really love to see a tutorial for this too.
João Paulo Porto
i have the same question
João Paulo Porto
If for some reason, pagination is not showing up after you have pasted the next page tags, then you would need to add the following code in your single.php loop.
Which code are you talking about? I really need this code.
Lester
Olá João Paulo,
Have you noticed how to manage pagination on wordpress long posts? This thread is not really helpful. I´m using wp 2.2.2 and I´m looking for splitting long posts in 1,2,3,4…view all pages too !
WPBeginner Staff
See how to add numeric pagination to WordPress themes.
Josh
how to create pagination like wpbeginner.com ? thanks
Ameet Mehta
Hi, where is the code that is supposed to be pasted, seems like something got pulled out of the article?
kankan929
YES!!!! I saw that Kim Komando did this and wondered HOW. So glad I stumbled across this blog. And now I’m a FAN! Thanks for sharing this information.
WPBeginner Staff
Yes it does if you have long articles with lots of images. You split the page, which reduces the page load time. Increased page views and lower bounce rates are an added bonus.
MikeMeisner
Great little tip – do you think this helps with SEO and rankings by lowering the bounce rate and increasing pageviews? I notice a few buzzfeed types sites using this method..
Donna
what is a single.php loop? where do I place that code? the pagination is not working for me.
Jamie_Mannion
I paste the code in the text view, switch to visual and it’s there as I pasted it, switch back to text and it shows as <!––nextpage––> the problem was the “pasting”. I manually typed it and I was away. Thanks guys!
Patrick
Hi Syed,
Thanks for the tip. I’m wondering, though, the page numbers come up at the top of the post, rather than following it. How can I change that, or at least duplicate it?
Bonnie Martin
Awesome tip. I didn’t know about that before this.
James
Hi Syed,
I have just implemented a facebook like button at the top of every post page. and split a few long blog posts up into multiple pages.
The problem is if someone is on page 3 of the article for example, and clicks the share button, the url of that page gets shared – nameofsite.com/nameofpost/3.
How can I ensure that just the first page/main page of the post gets shared with all my paginated posts?
Thank you,
James
Boby Kurniawan
You know , i always love this website. I found many wordpress trick here. Thank you .
I have a question, how i put the “split” at top of article after the title ? is it posible ? thanks .
Sorry for bad english
Basavaraj Tonagatti
Hi,
I have few posts which have plenty of comments like around 800. Because of this these particular posts load slowly. So how if I paginate them by going to Discussion Settings–>Other Comments Settings–>Break Comments into pages of 100 each?
Lops
Hey! This worked incredibly fine, replacing the — manually did fix it when it didn’t work and now it’s awesome.
I’m just having trouble because I’m working on very lenghty articles and I would like a table of contents at the top of the page too, not just at the bottom of the page. Can’t we have the [1] [2] [3] etc. links at the top of the page too?
ashutosh joshi
I need to show “next page” and “previous page” in place of pagination. What should I do for that?
David
Hi Syed,
Thanks for the tip. I have a question to be sure.
This will create duplicate content, as http://domain.com/postname, http://domain.com/postname/1/, http://domain.com/postname/2/.
Would it be correct to add, for example using the SEO Yoast plugin, the canonical url at http://domain.com/postname?
Would this reduce any problem for duplicate content in the major search engines?
Thank you.
WPBeginner Support
WordPress SEO will make the actual post URL the canonical URL.
Admin
David
You mean, without writing anything in the canonical url space? Does it do it automatically so that I don’t have to specify it?
Thanks
David
Hi,
After a bit of investigation, I’ve found out that if you don’t write anything on WPSEO canonical space, wordpress will take care of it and create a different canonical url for each page, with duplicate content. It doesn’t play nice with all the themes probably, so it’s better to check.
So if you write the right canonical url (usually the main page) in the WPSEO space, it will index the first and not the others and will relate all the others pages /2, /3.. to the first. And this is one solution.
But if you want to index all the content of the other pages, because maybe they are worth it and long pages as well, then you can write “next” on the canonical space, and all the pages will be linked as rel=”next” and rel=”prev”.
Edward Chung
Thanks for introducing the technique. What I concern most is the SEO implication, would the author please suggest whether the SEO would be hurt or not? Thanks!
WPBeginner Support
No, if any thing it will probably improve SEO. Your page load time will increase, users will not have to scroll a lot this means user experience will improve. A Better user experience is also one of the factors considered by search engines when ranking a site. Using post pagination correctly will benefit your site’s SEO. However, using it just to increase page and ad impressions will probably backfire.
Admin
Oscar Gonzalez
Do you know of a plugin or a hack that would allow me to give the user an option next to the pagination links when using multiple pages?
Like page 1, 2, 3,
OR below that show a link that reads:
view as one page
I think some big sites do that with slideshow posts, Any suggestions on providing that to the user?
Thanks!
Crear Cuenta Outlook
thank for the info i will use this in my site, but how i can get pagination on the home page?
WPBeginner Support
Here is how to add numeric pagination in your WordPress theme.
Admin
Crear Cuenta Outlook
thanks
Kalyan
I being having a travel blog (wordpress platform), thought of splitting the article. But, by using the method you said above, the url of the page is changing for each split. Is there any plugin or any thing which can split the article with the url remaining the same. Please let me know if you know any such plugin.
Thanking You
WPBeginner Support
You can take a look at toggle effect to show/hide content in a post.
Admin
Diana
The pagination shows up, but whenever I click to an actual page, it still shows me the entire article.
Laurence
I leave blogs split over many pages they’re really annoying. I can’t scan the page so it takes too long. Especially the blogs that have. “Top 10 whatever” with each one on its own page. Just put them on one page for me why on earth make it harder for me to get content. I don’t think split pages decrease the average bounce rate across all pages.
Aslam
I saw a lot of people complaining that the code tags aren’t working and the reason is that if you copy paste the on this page it will not work, maybe some character issue with the “–” characters on this page.
Just manually type the “–” wherever you are using the tag and it will work.
Manual typing worked for me.
Kristof Bernaert
Exactly the problem I faced too. Thanks for posting that!
James Roland
Thanks! That was my problem as well. Typing it manually did the trick
Aristides Guerra
I almost gave up upon manually replacing the underscores ( _ ) from the code given above but then I also replaced the two dashes( — ) from
and it works! thank you all!
Seema
Thanks Aslam, you solved my problem.
Tor André Sandum
THANKS! Manually writing worked, copy/paste did not!
John
@Syed Balkhi I have to agree with AleC that original post split looks very boring. Please write a detailed tutorial for a newbies like us, on how to give it a beautiful and stylish looks with eye catching colors, just like you are using at list25. Thanks and i hope you will share it soon with your regular reader. I will wait
WPBeginner Support
We will try to show how to style WordPress post pagination links. Meanwhile, do check the Codex page for styling page links. Also feel free to study and use list25 stylesheet and modify it to match your theme.
Admin
Haseeb Ahmad Ayazi
Whenever I google any wordpress query, wpbegginner come first, very hard @Syed Balkhi
Christina
Thank you for your answer. That makes a lot of sense. One more question: Do you know a post pagination plugin with works in combination with a post index? I have some long posts on my website which have their own little post index. If I now implement a post pagination, I would like to keep the post index which means that if a user klicks on a post index element, he should then jump to a separate post sub page.
Christina
Does post pagination have any impact on site performance/loading time? I was told not to implement it because it slows down the website. Is this true?
WPBeginner Support
The purpose of adding pagination is to break down lengthy posts into pages. It should in fact speed up the page load time.
Admin
Lauren Wilson
Is it possible to have two posts pages? i.e news and jobs?
Sri Ganesh.M
Not Working, After which line in single.php we should add it ! i added in HTML view only
Kenshin
Does this work on wordpress.com blogs also?
Editorial Staff
Yes it should.
Admin
rami
YUP!!!It Worked.Thanks for your great contribution.
Pranjal
I thought, it wasn’t working on mine, lately I read it somewhere else, I need to put the given tag into html view, and finally it worked. Please mention in your article as well, as I know many noobs like me are out there
rami
I agree with Pranjal. Please mention where the tag to be place.
Editorial Staff
Updated the article.
Admin
Jose Robles
Tried it but my links for the other pages shows up at the way bottom left of my website rather than appearing even before the comments. Any ideas why that would be? Website is ReignMediaLA.com and the theme is Press Grid.
Editorial Staff
Sounds like an issue with your theme’s styling.
Admin
Eva
Never mind..
Of course it worked AFTER I’d tried for half an hour and finally decided to complaint.
Eva
I’ve tried to use the code but all I get is the code text in my post :/ I’ve only used the HTML window to place the code and yet – there it is – on my post as text, not as next page.
What can I do?
AleC
Hi guys,
Don’t ask me how, but I manage to do this in my site and it works like a charm!
BUT I don’t know how to give the numbers a style. I’m looking for something like you did in here, big numbers with a huge box of color. Can you help me with this? May be if you give me the line of code you used.
Sorry if I sound silly, but I don’t really know code.
Please!
Editorial Staff
There is no code involved. You have to know CSS formatting.
Admin
Gidon
Great! And so easy! Thank you!
Tom
It wont work even if you follow these instructions, the correct code is ‘ not as you said (you had only single dashes) – also you should tell people that it needs to be entered in html view on visual.
Editorial Staff
Ah darn the auto-formatting. It was showing correctly in the backend, but then on the front-end it turned our two dashes into one big dash. Fixed that. Thanks for pointing it out.
Admin
Colin
Darnit, tried to get this to work on my site but failed
Was hoping as it was a premium theme it would work out of the box but sadly not.
As an SEO I can say there should be no problem with this SEO-wise. If anything having an extra couple of pages won’t hurt.
Raja
Hi,
I tried what you’ve said, but ot still doesnt work on my theme. i’m using goodnews theme from themeforest
Editorial Staff
Hey Raja,
This is a standard WordPress feature. If it doesn’t work with your theme, then you should contact the theme author and ask them to add the support for it.
Admin
wpbeginner
You know Stephen, I would have agreed with you on almost all of those cases a few months ago. I still do agree with you that this works only in very specific cases. However, after seeing the numbers on our new site, my perspective has changed a little bit. First of all, if your article is good enough, then the user will go to the next page. In terms of SEO, definitely not true. If you have sufficient amount of content on each page, then it will not hurt you in SEO for a single bit. Forbes, NYTimes, and countless other big name sites do this and rank perfectly fine for SEO. If your content is good, then it will be shared, it will be linked, and it will be read by your users.
FuturePocket
@wpbeginner I agree, I am planning to write a three part article (which is going to be somewhere in the area of 5000+ words) and I really don’t want to fit it all into one page. I am contemplating whether to stick with pagination or split it into multiple articles — but I will have to do a little bit more keyword research before I decide. If the ideas I intend to discuss are in a wide variety of keywords, than I’ll probably split it, otherwise this pagination method will work out quite nicely! Thanks for the share.
YuriyNikolaev
Thanks God for give us WPBeginner!
Stephen Cronin
Thanks for telling us how to do this, but I hope not too many people actually implement it and split their posts.
That’s a relic of the days when people artificially increased their page views to increase advertising revenue, but thankfully most people these days recognise that it leads to a poor user experience. I personally leave sites as soon as I see paged articles (unless I really *have* to read it).
There’s also the SEO implications – you’re probably going to rank better with one long article than you would with 5 smaller pages.
And I could go on, but I’ll stop there. It’s not a good idea in 99.9% of cases.